Mathematics

At Wayne RESA we believe every student deserves to engage in meaningful learning experiences, in classrooms where teachers position them as capable to innovate, create, and think mathematically and who highlight students’ particular contributions to the classroom community. We support teachers and schools in designing learning experiences that enable all learners to thrive in school, in their community, and in the world.

Essential Instructional Practices for Elementary Mathematics

Essential Practices for Disciplinary Literacy

Meaningful Math and STEM Showcase

Planning for Ambitious Tier I Instruction

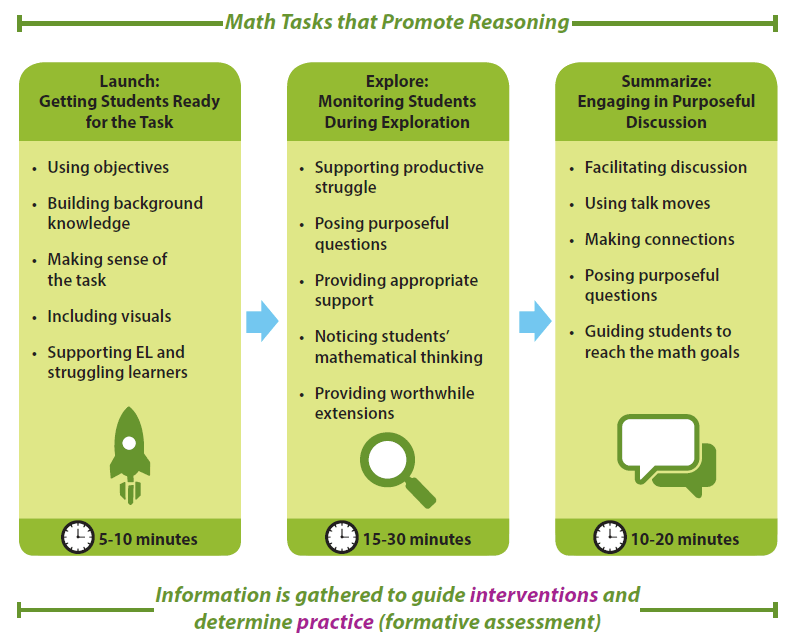
The Thinking Through a Lesson Protocol (TTLP)(Word Document, opens in new window) is used to guide teachers in thinking deeply about a specific lesson. The goal is to move beyond a basic lesson plan toward a deeper consideration of how to advance students’ mathematical understanding.

Part 1 of the TTLP lays the groundwork for planning before implementing rich math tasks. First, identify the learning targets. Then, select a high cognitive demand math task(PDF, opens in new window) aligned to the targets. Next, determine how to launch the task to help students make sense of the problem by activating prior knowledge and deciding which instructional tools will be available.

Part 2 of the TTLP helps monitor students during the Explore Phase. Prior to implementation, anticipate strategies and misconceptions students may encounter. Based on these, formulate questions to clarify and assess student thinking. The rest of the monitoring tool(Word Document, opens in new window) can be completed while recording the names of students using anticipated strategies. This helps in selecting and sequencing students for the Summarize Phase.

Part 3 of the TTLP focuses on orchestrating a whole-group discussion. This discussion uses different solution strategies to highlight the mathematical ideas of the lesson. Strategically plan the order of presentations to develop understanding and create questions that bridge connections between different student strategies.

Facilitating Meaningful Mathematical Discourse

“Effective teaching of mathematics facilitates discourse among students to build shared understanding of mathematical ideas by analyzing and comparing student approaches and arguments.” (Huinker & Bill, 2017).

To facilitate this, teachers must establish norms for discourse(PDF, opens in new window) to create a safe environment and ensure equitable participation. Additionally, productive talk moves(Word Document, opens in new window) can be used to engage all students in meaningful discussion.

When determining which talk move to utilize, consider the specific instructional goal you are trying to achieve based on student responses:

Clarifying: Helping individual students clarify and share their own strategies.
Orienting: Helping students orient to the thinking of other students.
Deepening: Helping students deepen their own mathematical reasoning.
Engaging: Helping students to engage with the reasoning of others.

Web Resources

$Inside Mathematics resource flyer showcasing professional development tools for educators$

Inside Mathematics(opens in new window)

A professional resource for teachers, coaches, and administrators passionate about improving students’ mathematics learning and performance. This site includes classroom videos, tower of tasks, and performance assessment resources aligned to the Common Core State Standards.

Book Resources

Taking Action: Implementing Effective Mathematics Teaching Practices (K-5)
ISBN-13: 978-0873539692

Taking Action: Implementing Effective Mathematics Teaching Practices (6-8)
ISBN-13: 978-0873539753

Taking Action: Implementing Effective Mathematics Teaching Practices (9-12)
ISBN-978- 0-875353-976-0

Children's Mathematics: Cognitively Guided Instruction (Whole Number Operations)
ISBN-13: 978-0325052878

Extending Children's Mathematics: Innovations in Cognitively Guided Instruction (Fractions and Decimals)
ISBN-13: 978-0325030531

Framework for Ambitious Instruction

NCTM has identified eight Mathematics Teaching Practices(PDF, opens in new window) that research indicates are consistent components of every mathematics lesson. Learners should have experiences that enable them to "engage with challenging tasks... connect new learning with prior knowledge and informal reasoning... acquire conceptual as well as procedural knowledge... construct knowledge through discourse, activity, and interaction with meaningful problems... receive descriptive and timely feedback... and develop meta-cognitive awareness of themselves as learners, thinkers, and problem solvers" (NCTM, 2014, p. 9).

Based on these principles, Wayne RESA has created a Framework for Ambitious Instruction(PDF, opens in new window).

$Wayne RESA Framework for Ambitious Instruction showing the intersection of teaching practices, student engagement, and mathematical tasks.$

An excellent mathematics program ensures that assessment is an integral part of instruction, provides evidence of proficiency [for teachers and students] of important mathematics content and practices, includes a variety of strategies and data sources [which are instructionally sensitive], and informs feedback to students, instructional decisions, and program improvement.”

(NCTM, 2014, p. 89)

Assessment to Inform Instruction

Assessment to Inform Instruction supports teachers in answering the critical question: What comes next in learning?

Effective methods of assessment for learning include listening to student contributions—both their responses and the questions they ask peers and teachers—as well as analyzing written work. This information allows teachers to interpret student understanding and determine precise instructional next steps.

$Student work sample showing the multiplication of 16 ounces by 5 pounds using a standard algorithm to reach 80 ounces.$ The student work sample shown here demonstrates that the learner recognizes there are 16 ounces in a pound and understands the multiplicative nature of the problem. Furthermore, the student utilizes a formal algorithmic method for solving 16 x 5, moving beyond more basic strategies like counting by 5s or repeated addition.

In elementary mathematics, researchers have developed learning progressions that describe the likely development of student mathematical thinking for "Big Ideas," such as addition, subtraction, multiplication, and division. These progressions guide teachers in making instructional decisions based on a student’s current progress.

K-5 Whole Number Concept Progressions:

Diagnostic Assessment

$1st Grade Math Spring Screener video thumbnail showing an interview-based assessment session.$

Diagnostic Assessment can be used to identify students’ strengths as well as areas for improvement. This data forms the basis for interventions and is often shared with multiple educators to plan supports that improve student learning.

This short interview-based assessment video(opens in new window) provides the teacher with information related to students’ understanding of number, addition and subtraction, place value, and multiplication. It can be used to determine if a student is performing at grade level and to identify specific areas of strength or weakness.

Interim (Unit Assessments)

Interim (Unit) Assessments support teachers in answering the questions Which standards are our students consistently not mastering? Where can we improve instruction? Which students need specific help? (Stiggins, 2010).

Interim assessments should identify content standards that students are struggling to master as well as the students struggling to meet those standards. Teachers can use this information to improve their own instructional practices aimed at those standards. Additionally, these assessments can help teachers and students focus on identifying student strengths and areas of improvement so they can intentionally plan interventions.

Assessment of Learning

Assessment of Learning supports teachers, schools, and districts in answering critical questions: What standards are our students consistently not mastering? Where and how can we improve instruction next year? (Stiggins, 2010).

Summative assessments evaluate student learning against intended outcomes. These assessments provide evidence of student achievement and can identify the percentage of students meeting performance expectations on state content standards (Chappuis, 2015).

In Michigan, students are assessed summatively in the spring of each year, starting in 3rd grade. The MDE provides access to Sample Assessment Items for 3rd–7th Grade M-STEP(opens in new window).

Secondary students are assessed using the PSAT or SAT(opens in new window). Released items from these exams can be used in a variety of ways to inform the work that students are doing in the classroom.

Book Resources

Professional Learning Resources: Math Assessment and Intervention

Resource Image	Title and ISBN
$Book cover of The Formative 5: Everyday Assessment Techniques for Every Math Classroom$	The Formative 5: Everyday Assessment Techniques for Every Math Classroom Authors: Fennell, Kobett, & Wray ISBN-13: 978-1506337500
$Book cover of Teaching Number in the Classroom for 4-8 year olds$	Teaching Number in the Classroom for 4-8 year olds (Assessment and Intervention) ISBN-13: 978-1446282694
$Book cover of Developing Number Knowledge for 7-11 year-olds$	Developing Number Knowledge: Assessment, Teaching, and Intervention with 7-11 year-olds ISBN-13: 978-0857020611

A mathematics curriculum is more than a collection of activities; instead, it is a coherent sequencing of core mathematical ideas that are well-articulated within and across grades and courses. Such curricula pose problems that promote conceptual understanding, problem-solving, and reasoning, and are drawn from contexts in everyday life and other subjects (NCTM, 2014, p. 72).